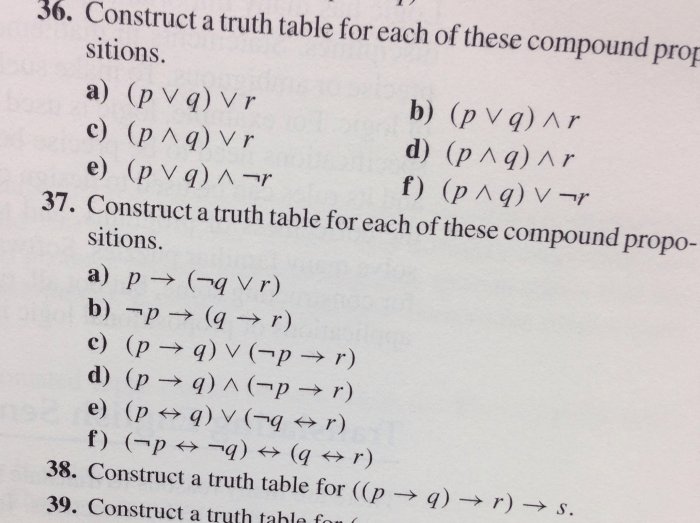Construct a truth table for each of these compound propositions – Constructing truth tables for compound propositions is a fundamental aspect of propositional logic, providing a systematic approach to evaluating the truth value of complex statements. This comprehensive guide delves into the intricacies of compound propositions, truth tables, and logical operators, empowering readers to analyze and understand the behavior of compound propositions with precision.
By exploring the concepts of logical equivalence and the step-by-step process of constructing truth tables, this guide offers a clear and concise understanding of this essential logical tool. Whether you are a student of logic, mathematics, or computer science, this guide will equip you with the knowledge and skills to confidently construct and analyze truth tables for compound propositions.
Defining Compound Propositions
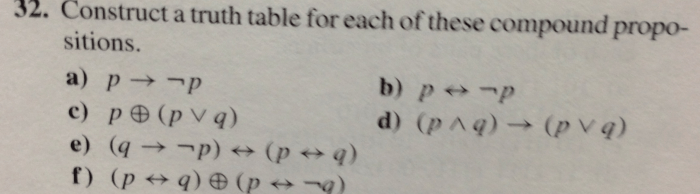
Compound propositions are statements that combine multiple propositions using logical operators to create more complex statements. They allow us to express relationships between propositions and build more sophisticated logical arguments.
For example, the compound proposition “If it is raining, then the ground is wet” combines the propositions “It is raining” and “The ground is wet” using the logical operator “if-then”.
Constructing Truth Tables, Construct a truth table for each of these compound propositions
Truth tables are a systematic way to evaluate the truth value of compound propositions for all possible combinations of input values. They consist of a table with columns for each proposition and rows for each possible combination of truth values.
For example, the truth table for the compound proposition “If it is raining, then the ground is wet” would have two columns, one for “It is raining” and one for “The ground is wet”, and four rows, one for each possible combination of truth values (true/false).
Logical Operators and Their Truth Values
The logical operators used in compound propositions are AND, OR, and NOT. Each operator has a specific truth value for each possible combination of input values.
| Operator | Input 1 | Input 2 | Output |
|---|---|---|---|
| AND | True | True | True |
| AND | True | False | False |
| AND | False | True | False |
| AND | False | False | False |
| OR | True | True | True |
| OR | True | False | True |
| OR | False | True | True |
| OR | False | False | False |
| NOT | True | False | |
| NOT | False | True |
Creating Truth Tables for Compound Propositions
To construct a truth table for a compound proposition, follow these steps:
- List all the propositions involved in the compound proposition.
- Create a truth table with columns for each proposition and rows for each possible combination of truth values.
- Evaluate the truth value of the compound proposition for each row of the truth table using the truth values of the input propositions and the logical operators.
For example, the truth table for the compound proposition “If it is raining, then the ground is wet” would be as follows:
| It is raining | The ground is wet | If it is raining, then the ground is wet |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | True |
| False | False | True |
Analyzing Truth Tables
Truth tables can be used to analyze the truth value of compound propositions and to determine their logical equivalence.
Logical equivalence occurs when two compound propositions have the same truth value for all possible combinations of input values. For example, the compound propositions “If it is raining, then the ground is wet” and “The ground is wet if it is raining” are logically equivalent because they have the same truth value for all possible combinations of truth values.
FAQ Insights: Construct A Truth Table For Each Of These Compound Propositions
What is a compound proposition?
A compound proposition is a statement that is formed by combining two or more simple propositions using logical operators such as AND, OR, and NOT.
What is the purpose of a truth table?
A truth table is a tabular representation that shows the truth value of a compound proposition for all possible combinations of truth values of its component propositions.
How do I construct a truth table for a compound proposition?
To construct a truth table for a compound proposition, you need to list all possible combinations of truth values for the component propositions, and then evaluate the truth value of the compound proposition for each combination.
What is logical equivalence?
Logical equivalence is a relationship between two compound propositions that have the same truth value for all possible combinations of truth values of their component propositions.